RNN: Backpropagation

RNN

RNN의 Backpropagation에서의 Gradient Vanishing/Exploding 문제에 관해 정리한 글입니다.

Gradient Vanishing

 

RNN은 $h_t = tanh(w_{xh}x_t+w_{hh}h_{t-1}), y_t = g(w_{hy}h_t)$ 로 나타낼 수 있다. 여기서 학습해야 하는 파라미터는 $w_{xh}, w_{hh}, w_{hy}$ 세가지 이다. 세 가중치는 매 시점에서 각각 동일한 값을 갖는다.

 

$w_{xh}$와 $w_{hh}$의 gradient를 구해보면 다음과 같다. $w$의 gradient는 매 시점에서의 $w$가 Loss에 미치는 영향을 합산한 결과이다.

 

 

 

이 때, $h_t$는 $tanh()$이며, 도함수는 (0,1] 범위 안에 존재한다. 따라서, RNN의 네트워크가 깊어질수록, 앞 시점의 gradient가 소실된다.

 

Gradient Exploding

RNN의 Computational Graph를 생각해보자.

Backpropagation in RNN (출처: Backpropagation in RNN Explained. A step-by-step explanation of… ❘ by Neeraj Krishna ❘ Towards Data Science )

 

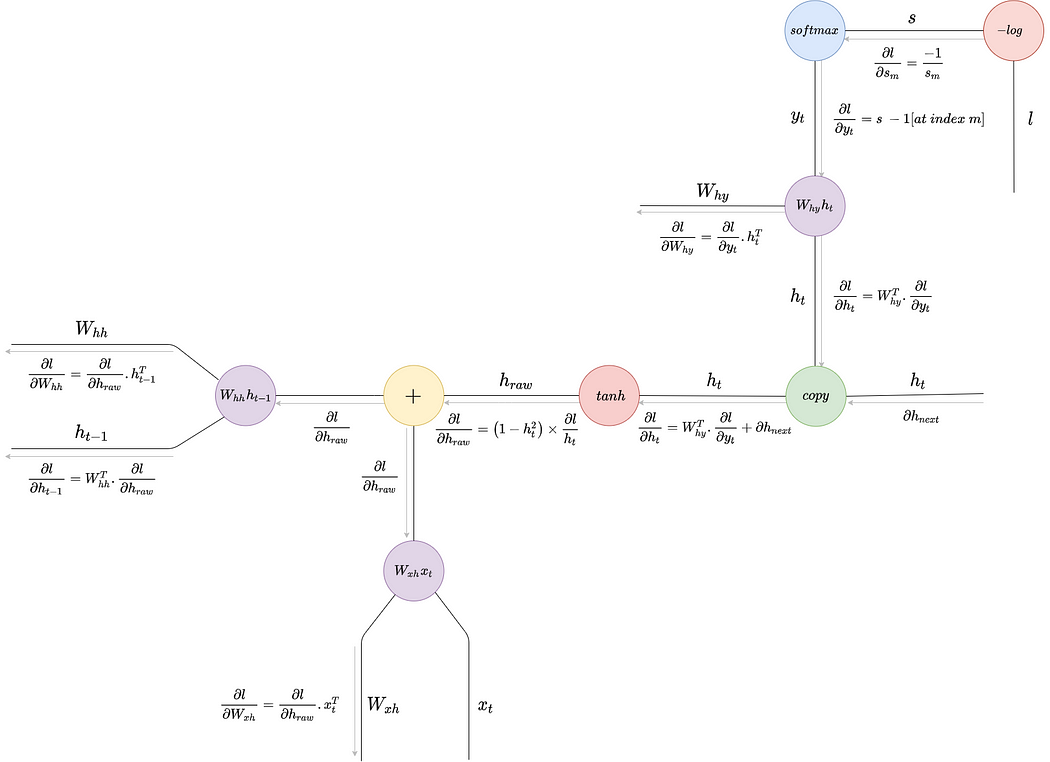
Backpropagation 과정에서 $h_{t-1}$ 방향으로 계속해서 gradient를 곱해나가야 한다.

 

$w_{hh}h_{t-1}$의 Mul-gate를 참고해보자. $h_{t-1}$방향으로의 local gradient는 $w_{hh}$ 이다.

 

따라서, Backpropagation 과정에서 RNN Cell 개수 만큼 $w_{hh}$가 곱해진다. 여기서 문제점은 매번 곱해지는 가중치가 같은 값이라는 점이고, 가중치의 값에 따라 gradient vanishiing/exploding 문제가 발생할 수 있다는 점이다. 

 

 

$W$ 행렬의 특이값(singular value)이 1보다 큰 경우 gradient가 아주 커지는 "exploding gradient problem"이 발생하게 되고,

 

 

$W$ 행렬의 특이값(singular value)이 1보다 작은 경우라면 gradient가 기하급수적으로 작아지는 "vanishing gradient problem"이 발생한다.