Stanford에서 강의하는 CS231n에 대해서 공부하고 정리한 글입니다.
Slide: cs231n_2017_lecture5.pdf
Convolutional Neural Networks
Fully Connected Layer vs Convolution Layer
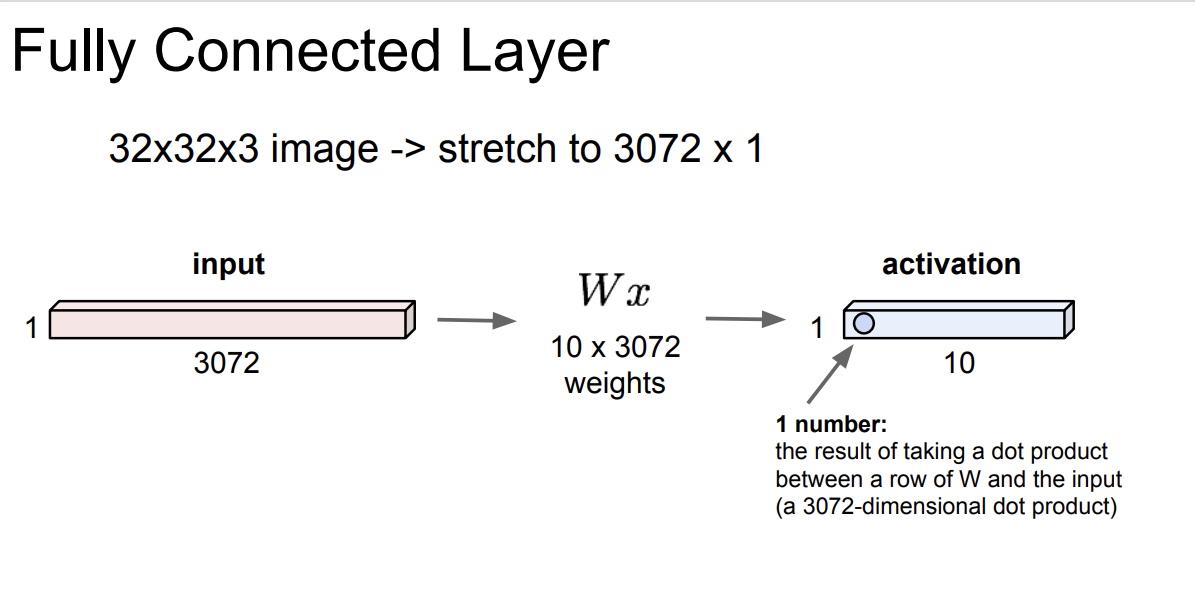
Fully Connected Layer와 Convolution Layer를 비교해보자.
FC Layer는 모든 입력이 결과에 영향을 미친다.
[32, 32, 3] 크기의 이미지가 존재한다면, 이를 [3072, 1] 크기의 벡터로 펼칠 수 있고 [10, 3072] 의 가중치 벡터를 만들어 가중합하여 [10, 1] 크기의 벡터를 만들 수 있다.
이는 [32, 32, 3] 이미지를 10개의 클래스로 학습한 것이다.
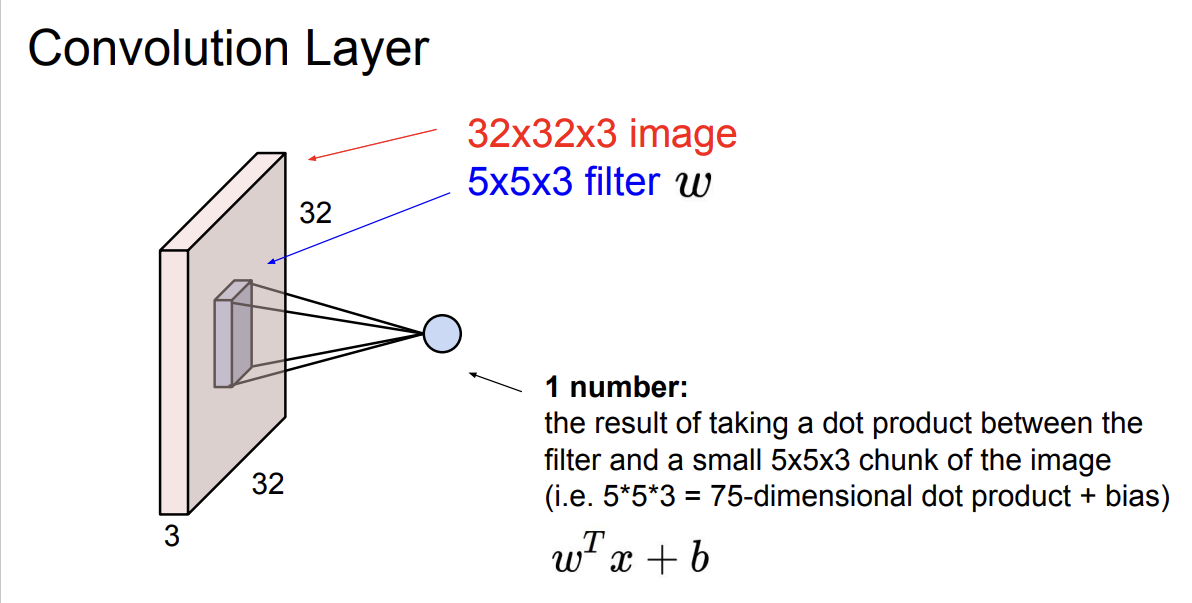
반면, Convolution Layer는 공간 구조를 유지한채 진행된다.
[32, 32, 3] 이미지를 보존한채로 [5, 5, 3](example) 필터를 통해 어떠한 값을 추출할 수 있다.
이 값은 [32, 32, 3] 이미지 내의 [5, 5, 3] 영역과 [5, 5, 3] 필터를 가중합 한 값이다.

이렇게 원본 이미지의 모든 영역을 이동(slide) 하면서 모든 영역에서의 특징을 추출하여 우측과 같은 activation map을 만들 수 있다.
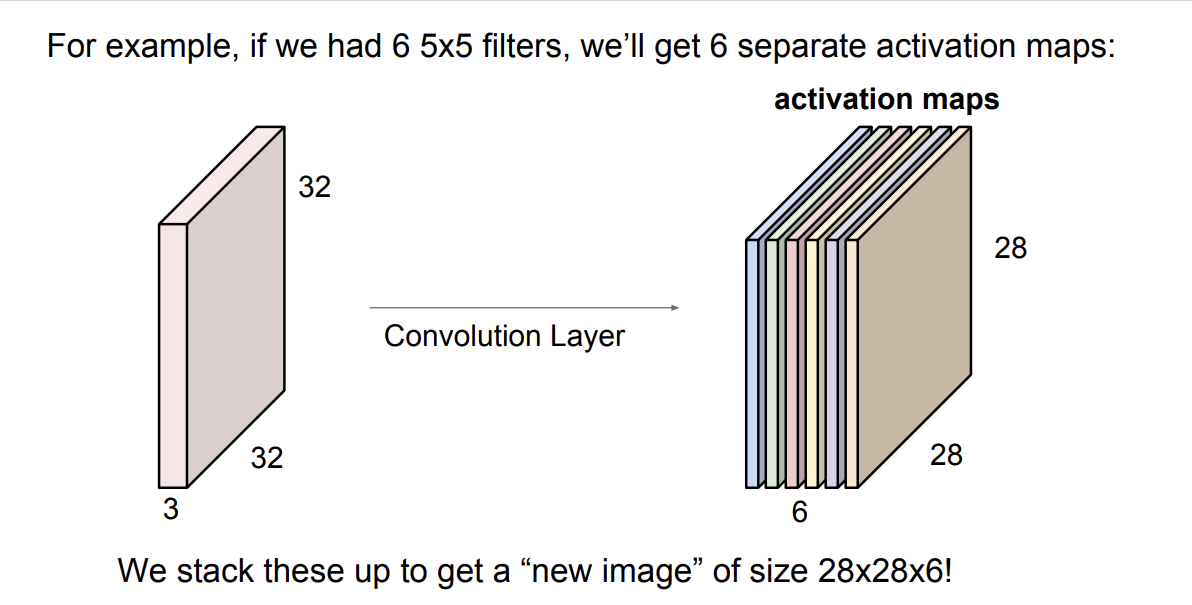
만약, N개의 필터를 사용한다고 한다면, N개의 activation map이 만들어 진다.
여기서 각 activation map은 입력 이미지로부터 추출한 다른 차원의 특징들이 된다.
만약, 자동차와 말을 분류하는 모델이라 가정한다면, 첫 번째 activation map은 왼쪽을 향한 말 이미지를, 두 번째 activation map은 오른쪽을 향한 말 이미지를 학습하게 된다.

Convolution layer는 Convolution 계산과 Activation Function으로 구성되어 있으며,
CNN은 이를 여러번 반복하여 계층적으로 쌓아올려 구성된다.
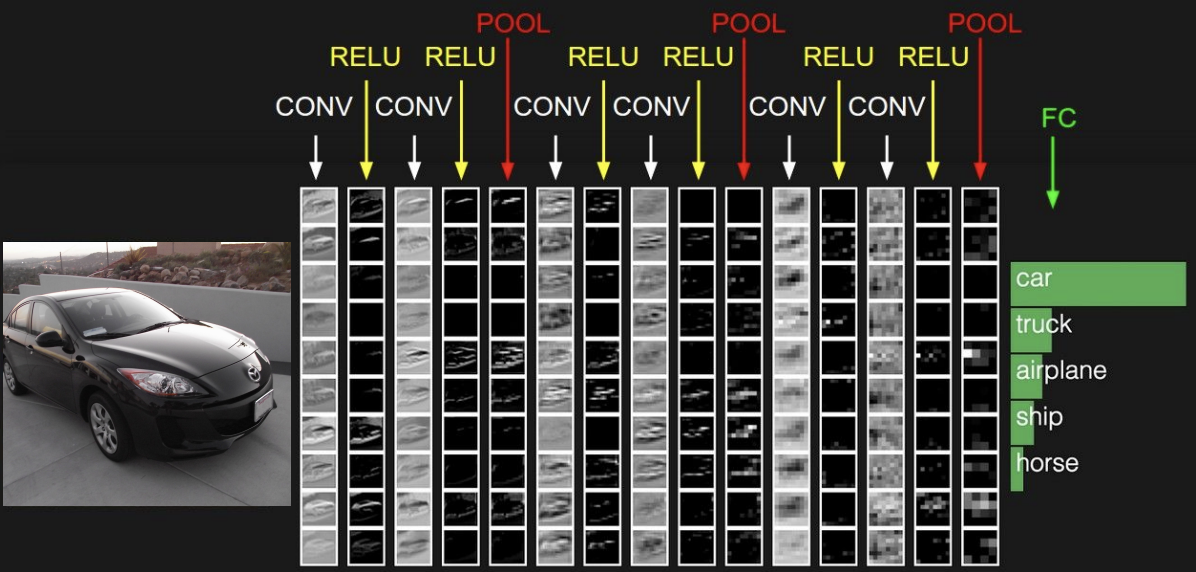
조금 더 자세히는
1) Convolution 계산과 Activation Function
2) Pooling Layer
의 반복으로 구성되며 마지막엔
FC Layer를 통해 원하는 output을 맞춰준다.
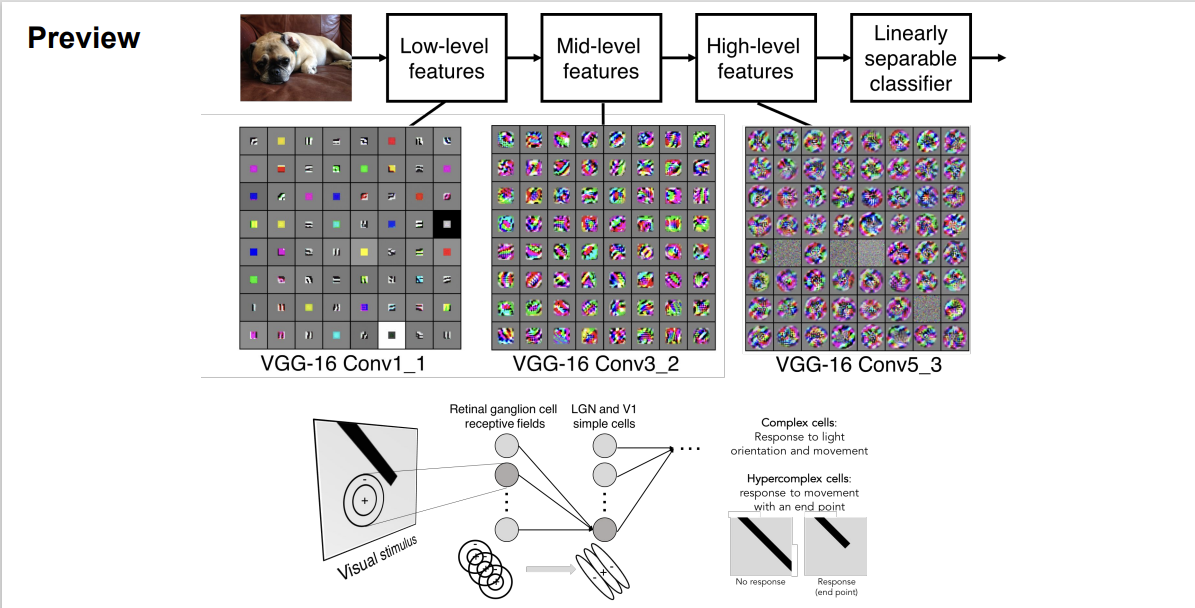
Convolution layer가 계층적으로 쌓이면서
초반의 layer에는 edge와 같은 Low-level feature가 학습된다.
점차 layer가 깊어지며 의미를 해석하기 힘든 High-level feature가 학습되고
이는 우리의 뇌에서 실제로 작용하는 구조와 유사하다.
A closer look at spatial dimensions

그럼, 입력 이미지와 필터를 통해 특징 맵을 뽑아내는 과정을 살펴보자.





입력 이미지는 [7, 7], 필터는 [3, 3]으로 예시를 둔다.
입력의 좌측 상단부터 시작하여
1) 필터와 입력간의 가중합을 구한다.
2) 우측으로 필터를 이동한다.
3) 필터가 이미지를 이탈하기 전까지 (1,2) 를 반복한다.
이러면 [7, 7] 이미지로부터 [5, 5] 크기의 activation map을 추출할 수 있다.
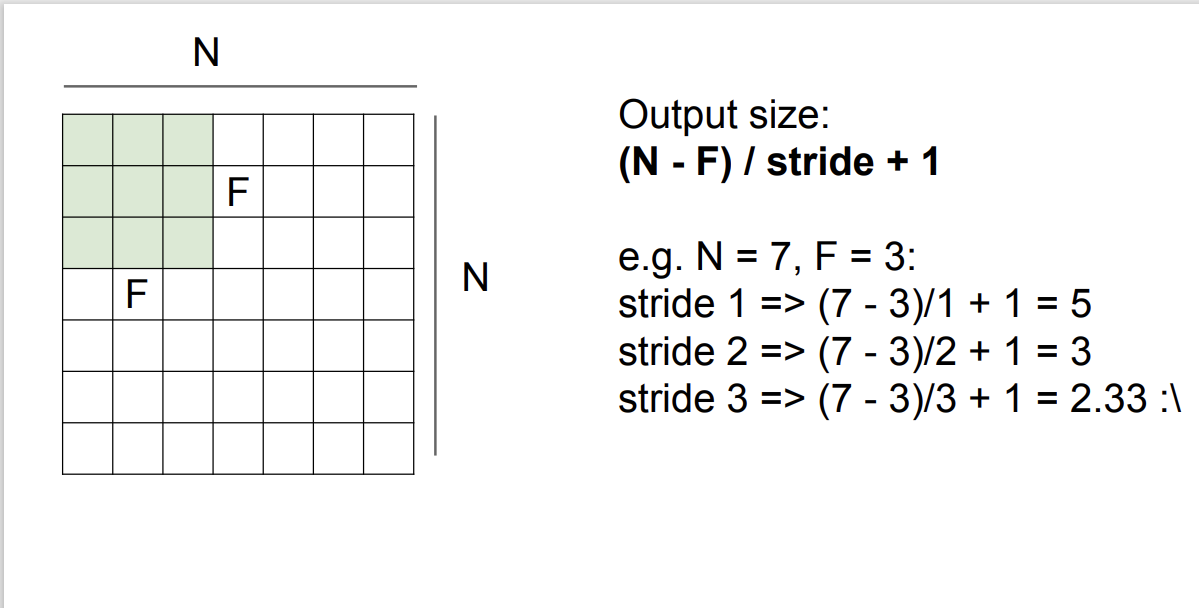
필터의 이동 간격을 Stride라 하는데, 이는 직접 지정해 줄 수 있는 하이퍼파라미터 이다.
입력 이미지 크기(N), 필터 크기(F), 필터 이동 간격(F)를 통해 우리는 Activation map의 크기를 구할 수 있다.

위와 같은 방법을 통해 Activation map을 구하다보면, layer가 반복될 수록 activation map의 크기가 작아지는 것을 알 수 있다. 따라서, 이를 방지하기 위해 Padding을 사용할 수 있다.
이러면, Activation map의 크기를 구하는 공식이 약간 바뀐다.
$Output Size : (N-F+2*P)/stride + 1$
입력 이미지가 $N$이 아닌, $N+2*P$ 라고 생각해보면 간단하다.

간혹, $1x1$ Convolution layer를 볼 수 있다.
이는 필터의 차원을 줄여주는 역할을 한다.
[1, 1, 64]와 [1, 1, 32]가 Fully Conntected 하게 연결되어 특징맵 크기를 줄여주고, [56, 56] 반복되며 새로운 activation map이 그려진다고 이해하면 될 것 같다.
[56, 56, 64]의 activation map이 존재한다고 가정하자. 이는 입력으로부터 64차원의 특징을 학습한 map이다. 하지만, 이를 FC layer와 연결하려고 생각해보면 200,704 개의 벡터와 Output Class 노드가 연결되어 학습해야하는 파라미터가 굉장히 많다.
따라서, $1x1$ Convolution layer를 통해 [56, 56, 32] 로 특징 맵을 줄여주면서 파라미터를 줄여줄 수 있다.
Pooling layer

우리는 Pooling layer를 통해서도 representation을 줄여줄 수 있다.
Pooling layer는 예시 이미지에서 보는것과 같이 downsampling 효과가 있다.

$2x2$ Max Pooling을 예시로 들면,
입력의 $4x4$ 이미지에서 각 $2x2$ 영역에서 대표 값(가장 큰 값)을 추출하여 그 값들로 새로운 이미지를 만든는 것이다.
전체 영역에서 대표 값들을 뽑아 재조합하므로 downsampling과 같다.
Fully Connected Layer

마지막으로, Classification을 위해 FC Layer를 사용한다.
이미지로부터 Convolutional layer를 통해 Activation map를 만들고, 이를 반복하며 마지막 layer에서 생성된 Activation map을 FC Layer를 통해 Class를 계산한다.
'Stanford CS231n' 카테고리의 다른 글
| Lecture 9: CNN Architectures (1) | 2024.11.11 |
|---|---|
| Lecture 7: Training Neural Networks 2 (1) | 2024.11.08 |
| Lecture 6: Training Neural Networks 1 (2) | 2024.11.08 |
| Lecture 4: Backpropagation and Neural Networks (0) | 2024.10.30 |
| Lecture 3: Loss Functions and Optimization (3) | 2024.10.28 |