Stanford에서 강의하는 CS231n에 대해서 공부하고 정리한 글입니다.
Slide: cs231n_2017_lecture7.pdf
Optimization
SGD



우리가 지금까지 배운 최적화 기법은 GD, SGD 가 있다.
SGD는 Mini batch 단위로 data loss를 계산하여 gradient를 업데이트하는 방법이다.
하지만, SGD 알고리즘에는 몇가지 문제점이 존재한다.
- 고 차원의 공간에서 Loss는 지그재그로 지저분하게(nasty) 움직인다.
- $w_1$과 $w_2$가 있다고 가정해보자. 둘 중 어떤 하나는 gradient가 작고, 하나는 gradient가 클 때 그림과 같이 loss가 움직이게 된다. 즉, 수평 축의 가중치가 변해도 loss가 천천히 줄어들고, 수직 축의 가중치의 변화엔 민감하게 반응한다. 따라서 수평 차원의 가중치는 느리게 업데이트되면서 loss가 지저분하게 움직이게 된다.
- local minima와 saddle point 문제
- loss 그래프에 굴곡이 있다고 가정해보자. 우리는 그 굴곡을 넘어서 더 낮은 loss를 찾아가야 한다. 하지만, local minima에 빠지게 되면 gradient가 0이므로 가중치 업데이트가 일어나지 않는다.
- loss에 여러 축이 존재할 때, 한 축으로는 loss가 줄어들지만, 다른 축에선 loss가 증가하는 문제가 발생할 수 있다. 이 지점을 saddle point라고 한다.
- Mini batch를 통한 loss 추정에서 발생하는 Noisy 문제
- SGD 알고리즘은 Mini batch를 통해 각 batch의 loss를 구하는데, 전체 데이터 loss에 대한 추정값이다.
SGD + Momentum

기존 SGD의 문제점들을 해결하기 위해 Momentum 이라는 방법을 사용한다.
Momentum은 현재 gradient의 방향만 고려하는 것이 아니라, 속도를 같이 고려하는 것이다.
코드를 살펴보면, $vx$ 변수에 현재까지의 $vx$와 $dx$를 더해준다. 이를 반복하며 $vx$에는 gradient 값이 누적된다.
$x += lr * dx$ 대신 $x += lr * vx$ 를 해줌으로써 gradient 뿐만 아니라, 속도도 함께 고려할 수 있게 된다.

이를 통해 local minima에 빠졌을 때 $vx$의 도움을 받아 빠져나올 수 있다.
또한, Poor Conditioning을 생각해보면 수직 방향의 변동은 Momentum을 이용해 상쇄시킨다. 이를 통해 수직 방향의 변동은 줄여주고 수평 방향의 움직임이 가속화된다.
오른쪽 이미지를 살펴보면, 파란색 라인은 SGD+Momentum 이고, 검은색 라인은 SGD이다.
기존에 Noise 때문에 지그재그로 이동하던 상황을 Momentum을 이용해 Noise를 평균화하여 조금 더 부드럽게 움직이는 모습을 확인할 수 있다.
Nesterov Momentum
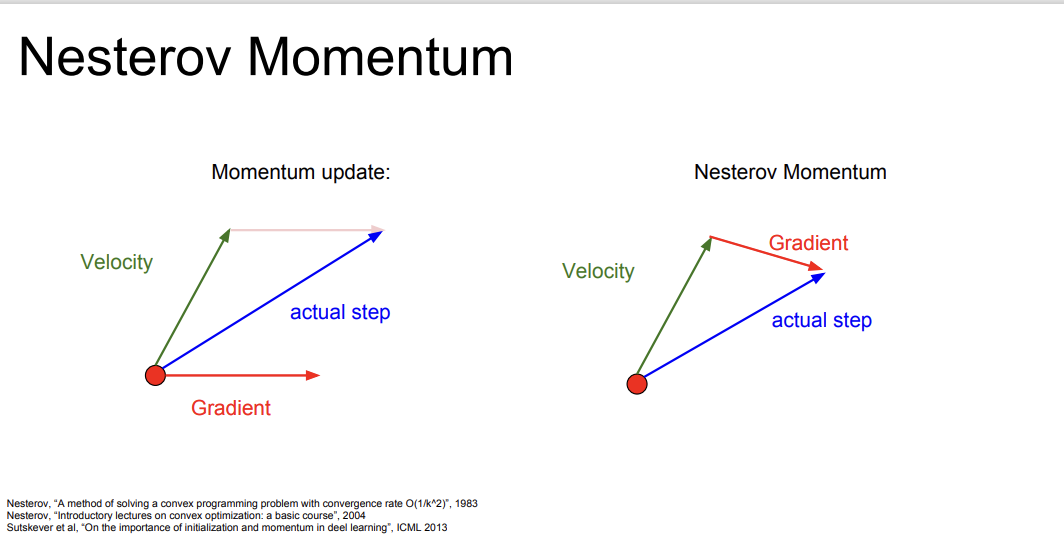
Momentum의 변형된 버전으로 Nesterov Momentum 방법도 존재한다.
계산 방법이 조금 바뀌게 된다.
기존의 SGD Momentum은 '현재 지점' 에서의 gradient와 velocity를 더해준 방향으로 actual step이 정해진다.
Nesterov Momentum은 '현재 지점'에서 velocity 방향으로 이동한 뒤, 그 지점에서의 gradient를 계산하여 더해준 방향으로 actual step이 정해진다.
AdaGrad

velocity 대신 grad squared term을 이용하는 방법도 제안되었다.
학습 도중 계산되는 gradient를 제곱해서 계속 더해준 뒤, update 할 때 update term을 앞 서 구한 gradient 제곱 항으로 나눠준다.
Small dimension에서는 gradient의 제곱 합이 작기 때문에 업데이트에 가속도가 늘어나고
Large dimension에서는 gradient의 제곱 합이 크기 때문에 업데이트에 가속도가 줄어든다고 한다.
Adagrad는 학습이 진행되면서 gradient의 제곱 합이 계속 쌓이게 되고 점점 learning step이 줄어들게 된다. 그런데, 이때 손실함수가 convex 한 경우는 상관없지만, non-convex 한 경우 local minima 혹은 saddle point에 걸려 멈춰버릴 수 있다.
이를 개선시킨 방법이 RMSProp이다.
RMSProp

RMSProp은 Adagrad의 gradient 제곱 항을 그대로 사용한다.
하지만, RMSProp은 decay_rate 변수를 통해 gradient 제곱 합의 스케일을 제어한다.
또한, 과거의 모든 기울기를 고려하지만, 매우 작은 비율이며 현재 기울기 정보를 더 크게 반영한다.
Adam

일반적으로 많이 사용되는 Adam을 많이 사용한다.
Adam은 Momentum 알고리즘과 Adagrad/RMSProp 알고리즘을 섞은 개념이라고 생각하면 된다.
코드를 살펴보면, first_moment는 Momentum을 구해준다.
second_moment는 gradient의 제곱을 누적시켜 더해가며 더해주며 AdaGrad/RMSProp과 유사하다.
한 가지, 추가된 부분이 있다면 Bias correction 부분이다.
초기 step에서 first_moment와 second_moment는 0으로 인위적으로 초기화해준 것을 기억해 보자.
second_moment를 1회 업데이트하고 난 후 값은 0에 가깝다.
이때, update step에서 second_moment로 나누어주면 초기 learning step이 엄청나게 커지게 된다.
따라서, 이를 보정하기 위해 Bias correction을 해준다.
Second-Order Optimization
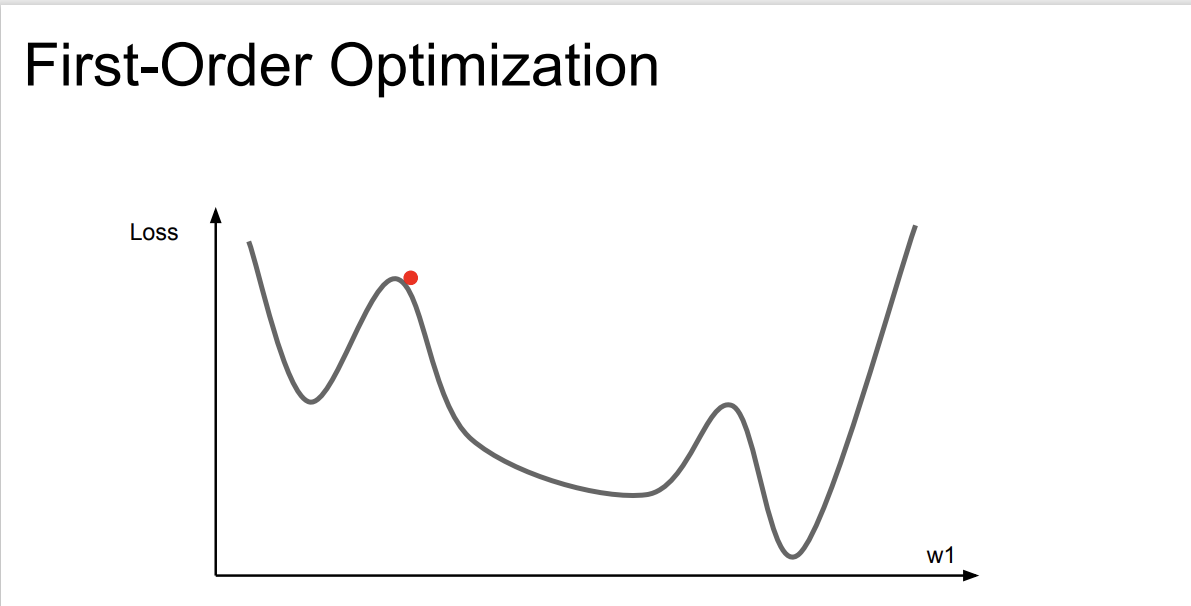
지금까지 알아본 Optimizer는 모두 1차 미분을 활용한 방법이었다.
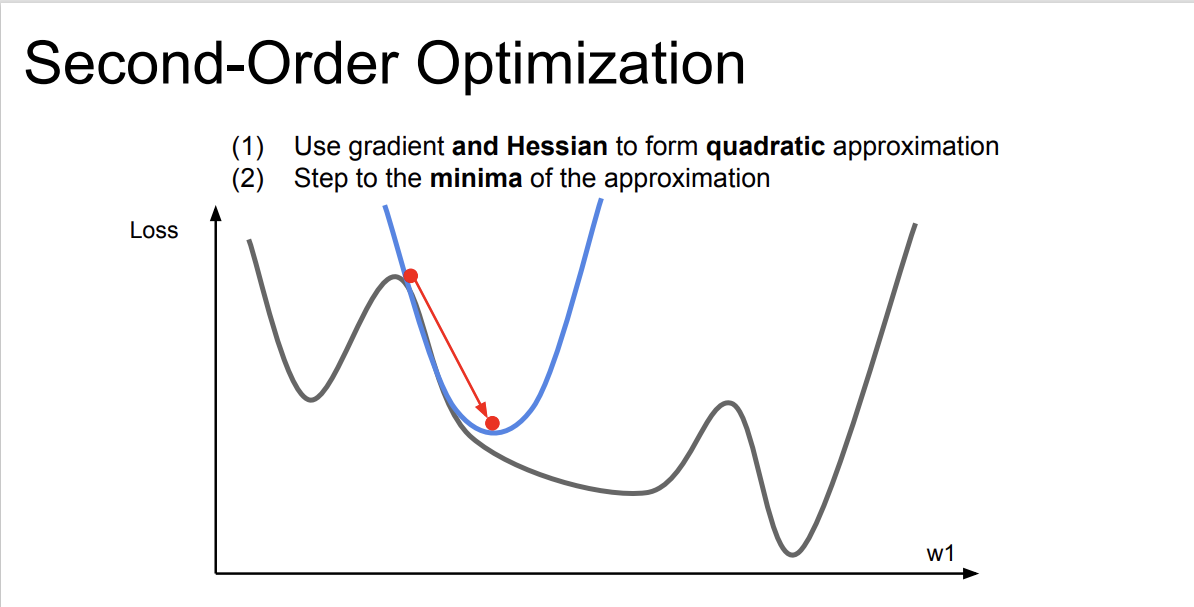
추가로, 2차 근사를 활용한 방법이 존재한다.

이를 다차원으로 확장시켜 보면 'Newton step'이라고 한다.
loss 함수의 2차 미분값들로 구성된 행렬인 Hessian matrix를 계산하고, Hessian matrix의 역행렬을 이용하면 minima로 바로 이동할 수 있는 아이디어라고 한다.
'Newton's method'라 불리는 이 방식에는 learning rate가 존재하지 않는다. 2차 미분을 통해 step마다 minima로 건너뛰기 때문이다.
하지만, Hessian matrix를 구하고 저장하며, 역행렬을 구하는 계산은 복잡(불가능?) 하기 때문에 이 방법을 사용하지는 않는다.
Hessian matrix를 구하는 것 대신 근사시키는 방법인 BGFS와 L-BGFS를 사용하는 방법이 있지만, 이 방법도 DNN에서는 잘 사용하지 않는다고 한다.
Regularization
Dropout
네트워크(모델)의 성능을 올리기 위한 방법 중 하나는 Regularization이다. 이는 training data에 과적합 되는 것을 방지하기 위한 정책이다. Regularization 방법에는 다양한 기법들이 있는데, 그중 Dropout에 대해 소개한다.

Dropout은 forward pass과정에서 일부 뉴런을 0(비활성화)으로 만드는 것이다.
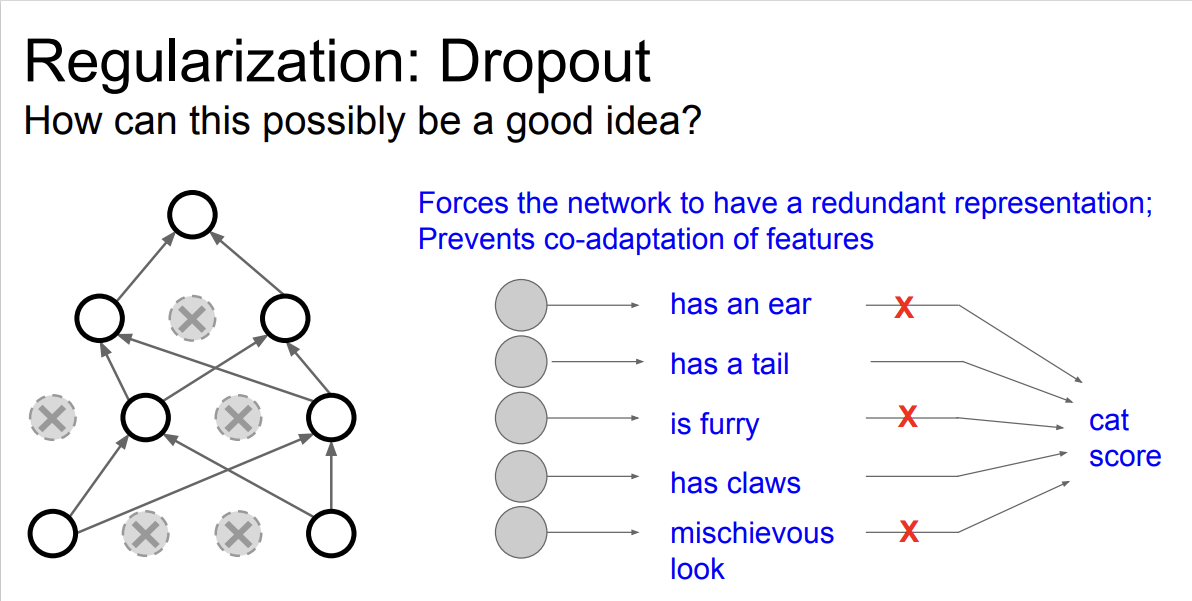
왼쪽에는 dropout이 없고, 오른쪽은 dropout이 적용된 경우이다.
매 iteration마다 그 모양은 계속 바뀐다.

구현 과정은 매우 간단하다.
Dropout은 실제로 좋은 성능을 낼 수 있게 도와준다.
그렇다면 dropout은 무슨 의미를 갖는 것일까?
강의에서는, 특징들 간의 상호작용을 방지한다고 본다고 한다.
예를 들어, 고양이를 분류하는 네트워크가 있다고 가정한다.
어떤 뉴런은 고양이의 귀에 대해, 어떤 뉴런은 꼬리에 대해, 어떤 뉴런은 눈에 대해 학습하는 것을 생각해 볼 수 있다.
dropout을 적용하게 되면 네트워크가 어떤 일부 특징들에게만 의존하지 못하게 하는 효과가 있다.
따라서, 모델이 '고양이' 라고 예측할 때 다양한 입력 특징들을 골고루 이용할 수 있도록 도와주며 Overfitting을 방지하는 효과가 있는 것이다.
이 뿐만 아니라, 다양한 관점에 따른 해석이 존재하는데 정리하지는 않는다.

Test time에서는 랜덤성을 주는 것은 옳지 않다. 따라서 dropout을 사용하지 않는다.
Training time에서 출력이 $a$ 이며, 입력이 $x, y$, 가중치 $w_1, w_2$ 가 있다고 가정해 보자.
$a$의 기대값으로 $\frac{1}{4}(w_1x+w_2y) + \frac{1}{4}(w_1x+0y) + \frac{1}{4}(0x+w_2y) + \frac{1}{4}(0x+0y) = \frac{1}{2}(w_1x+w_2y)$ 를 얻을 수 있다.
이 값은 $\rho * test time$ 이라고 생각해 볼 수 있다.

따라서, predict 에는 dropout을 적용하지 않고, activation layer 이후에 $\rho$ ($\rho$: dropout probability) 를 곱해주어 scaling 만 조절해 준다.

test time과 train time의 activation layer 출력의 스케일을 맞춰주기 위함이므로,
train time에서 activation layer 출력에 $\rho$를 미리 나누어도 좋다.
이렇게 되면 test time에서 계산량이 줄어들어 이득이라고 할 수 있다.
Data Augmentation
Overfitting을 막기 위해 데이터를 추가하는 방법을 사용할 수도 있다.
우리는 어떤 '고양이' 이미지를 갖고 있다고 생각해보자. 이 이미지는 상하좌우로 반전시켜도, 특정 영역을 잘라내도, 이미지 색이 약간 변경되어도 모두 '고양이' 를 나타낸다.
따라서, 앞서 말한 방법들을 통해 학습 데이터를 증강 시킬 수 있다.
Transfer Learning
Transfer Learning의 아이디어는 다음과 같다.
대량의 데이터셋으로 학습된 네트워크를 준비한다.
이 네트워크를 우리가 가진 작은 데이터셋에 적용한다.
가령, 1000개의 클래스를 분류하는 ImageNet으로 학습된 CNN 모델이 있다고 치자.
우리는 이 모델을 가지고 우리의 데이터셋(10종의 강아지)을 추가로 학습시켜 10종의 강아지를 분류하는 네트워크를 만들 수 있다.

물론, 네트워크의 마지막 레이어인 FC 레이어는 우리의 출력 클래스에 맞게 변경해 주어야 한다.
우리의 데이터셋으로 추가 학습을 하는 방법은 기존의 레이어들을 Freeze(가중치 업데이트가 일어나지 않게) 시킨 뒤 우리가 수정한 레이어에서만 가중치 업데이트가 일어나게 학습하는 것이다.
'Stanford CS231n' 카테고리의 다른 글
| Lecture 10: Recurrent Neural Networks (2) | 2024.11.11 |
|---|---|
| Lecture 9: CNN Architectures (1) | 2024.11.11 |
| Lecture 6: Training Neural Networks 1 (2) | 2024.11.08 |
| Lecture 5: Image Classification with CNNS (0) | 2024.11.05 |
| Lecture 4: Backpropagation and Neural Networks (0) | 2024.10.30 |