Stanford에서 강의하는 CS231n의 Assignment 2: Multi-Layer Fully Connected Neural Networks 를 정리한 글입니다.
Inline Question 1
Did you notice anything about the comparative difficulty of training the three-layer network vs. training the five-layer network? In particular, based on your experience, which network seemed more sensitive to the initialization scale? Why do you think that is the case?
Your Answer : 3-layer 모델이 5-layer 모델보다 학습이 쉬웠습니다. 초기화된 가중치가 너무 크거나 작으면, 기울기 소실 문제가 발생할 수 있습니다. 더 깊은 네트워크에서는 이런 문제가 가중되기 때문에 학습이 어려워집니다.
Inline Question 2
AdaGrad, like Adam, is a per-parameter optimization method that uses the following update rule:
cache += dw**2
w += - learning_rate * dw / (np.sqrt(cache) + eps)John notices that when he was training a network with AdaGrad that the updates became very small, and that his network was learning slowly. Using your knowledge of the AdaGrad update rule, why do you think the updates would become very small? Would Adam have the same issue?
Your Answer : AdaGrad는 각 가중치에 대해 기울기의 제곱을 누적 합으로 저장하며, 시간이 지남에 따라 이 누적합이 커지게 되면, 가중치 업데이트가 점점 작아지게 됩니다. 즉, $dw$가 커지더라도 cache도 동일하게 커지며 업데이트의 크기를 줄이게 됩니다. 이 방법은 학습이 진행되면서 학습이 느려지는 원인이 됩니다.
Adam은 momentum의 누적된 Velocity 만큼의 가중치 업데이트와 RMSProp의 기울기의 크기에 따른 학습률 조정 방법을 합친 알고리즘 입니다. 또한, Bias Correction을 통해 초기 가중치 누적 값들이 0에 가까운 점을 보정합니다. 이로 인해 Adam은 누적된 기울기의 크기에 의한 학습률 감소 문제를 완화하며, AdaGrad에서 발생하는 것처럼 학습률이 지나치게 작아지는 문제가 발생하지 않습니다.
Code
class FullyConnectedNet(object):
"""Class for a multi-layer fully connected neural network.
Network contains an arbitrary number of hidden layers, ReLU nonlinearities,
and a softmax loss function. This will also implement dropout and batch/layer
normalization as options. For a network with L layers, the architecture will be
{affine - [batch/layer norm] - relu - [dropout]} x (L - 1) - affine - softmax
where batch/layer normalization and dropout are optional and the {...} block is
repeated L - 1 times.
Learnable parameters are stored in the self.params dictionary and will be learned
using the Solver class.
"""
def __init__(
self,
hidden_dims,
input_dim=3 * 32 * 32,
num_classes=10,
dropout_keep_ratio=1,
normalization=None,
reg=0.0,
weight_scale=1e-2,
dtype=np.float32,
seed=None,
):
"""Initialize a new FullyConnectedNet.
Inputs:
- hidden_dims: A list of integers giving the size of each hidden layer.
- input_dim: An integer giving the size of the input.
- num_classes: An integer giving the number of classes to classify.
- dropout_keep_ratio: Scalar between 0 and 1 giving dropout strength.
If dropout_keep_ratio=1 then the network should not use dropout at all.
- normalization: What type of normalization the network should use. Valid values
are "batchnorm", "layernorm", or None for no normalization (the default).
- reg: Scalar giving L2 regularization strength.
- weight_scale: Scalar giving the standard deviation for random
initialization of the weights.
- dtype: A numpy datatype object; all computations will be performed using
this datatype. float32 is faster but less accurate, so you should use
float64 for numeric gradient checking.
- seed: If not None, then pass this random seed to the dropout layers.
This will make the dropout layers deteriminstic so we can gradient check the model.
"""
self.normalization = normalization
self.use_dropout = dropout_keep_ratio != 1
self.reg = reg
self.num_layers = 1 + len(hidden_dims)
self.dtype = dtype
self.params = {}
############################################################################
# TODO: Initialize the parameters of the network, storing all values in #
# the self.params dictionary. Store weights and biases for the first layer #
# in W1 and b1; for the second layer use W2 and b2, etc. Weights should be #
# initialized from a normal distribution centered at 0 with standard #
# deviation equal to weight_scale. Biases should be initialized to zero. #
# #
# When using batch normalization, store scale and shift parameters for the #
# first layer in gamma1 and beta1; for the second layer use gamma2 and #
# beta2, etc. Scale parameters should be initialized to ones and shift #
# parameters should be initialized to zeros. #
############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
tmp_dim=input_dim
for i in range(self.num_layers):
if i==self.num_layers-1:
self.params['W'+str(i+1)]=np.random.randn(tmp_dim,num_classes)*weight_scale
self.params['b'+str(i+1)]=np.zeros(num_classes)
else:
if normalization=='batchnorm':
self.params['W'+str(i+1)]=np.random.randn(tmp_dim,hidden_dims[i])*weight_scale
self.params['b'+str(i+1)]=np.zeros(hidden_dims[i])
self.params['gamma'+str(i+1)]=np.ones(hidden_dims[i])
self.params['beta'+str(i+1)]=np.zeros(hidden_dims[i])
tmp_dim=hidden_dims[i]
elif normalization=='layernorm':
self.params['W'+str(i+1)]=np.random.randn(tmp_dim,hidden_dims[i])*weight_scale
self.params['b'+str(i+1)]=np.zeros(hidden_dims[i])
self.params['gamma'+str(i+1)]=np.ones(hidden_dims[i])
self.params['beta'+str(i+1)]=np.zeros(hidden_dims[i])
tmp_dim=hidden_dims[i]
else:
self.params['W'+str(i+1)]=np.random.randn(tmp_dim,hidden_dims[i])*weight_scale
self.params['b'+str(i+1)]=np.zeros(hidden_dims[i])
tmp_dim=hidden_dims[i]
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
############################################################################
# END OF YOUR CODE #
############################################################################
# When using dropout we need to pass a dropout_param dictionary to each
# dropout layer so that the layer knows the dropout probability and the mode
# (train / test). You can pass the same dropout_param to each dropout layer.
self.dropout_param = {}
if self.use_dropout:
self.dropout_param = {"mode": "train", "p": dropout_keep_ratio}
if seed is not None:
self.dropout_param["seed"] = seed
# With batch normalization we need to keep track of running means and
# variances, so we need to pass a special bn_param object to each batch
# normalization layer. You should pass self.bn_params[0] to the forward pass
# of the first batch normalization layer, self.bn_params[1] to the forward
# pass of the second batch normalization layer, etc.
self.bn_params = []
if self.normalization == "batchnorm":
self.bn_params = [{"mode": "train"} for i in range(self.num_layers - 1)]
if self.normalization == "layernorm":
self.bn_params = [{} for i in range(self.num_layers - 1)]
# Cast all parameters to the correct datatype.
for k, v in self.params.items():
self.params[k] = v.astype(dtype)
def loss(self, X, y=None):
"""Compute loss and gradient for the fully connected net.
Inputs:
- X: Array of input data of shape (N, d_1, ..., d_k)
- y: Array of labels, of shape (N,). y[i] gives the label for X[i].
Returns:
If y is None, then run a test-time forward pass of the model and return:
- scores: Array of shape (N, C) giving classification scores, where
scores[i, c] is the classification score for X[i] and class c.
If y is not None, then run a training-time forward and backward pass and
return a tuple of:
- loss: Scalar value giving the loss
- grads: Dictionary with the same keys as self.params, mapping parameter
names to gradients of the loss with respect to those parameters.
"""
X = X.astype(self.dtype)
mode = "test" if y is None else "train"
# Set train/test mode for batchnorm params and dropout param since they
# behave differently during training and testing.
if self.use_dropout:
self.dropout_param["mode"] = mode
if self.normalization == "batchnorm":
for bn_param in self.bn_params:
bn_param["mode"] = mode
scores = None
############################################################################
# TODO: Implement the forward pass for the fully connected net, computing #
# the class scores for X and storing them in the scores variable. #
# #
# When using dropout, you'll need to pass self.dropout_param to each #
# dropout forward pass. #
# #
# When using batch normalization, you'll need to pass self.bn_params[0] to #
# the forward pass for the first batch normalization layer, pass #
# self.bn_params[1] to the forward pass for the second batch normalization #
# layer, etc. #
############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
cache={}
do_cache={}
out=X
for i in range(self.num_layers):
W=self.params['W'+str(i+1)]
b=self.params['b'+str(i+1)]
if i == self.num_layers-1:
out, cache[i] = affine_forward(out,W,b)
else:
if self.normalization == 'batchnorm':
gamma=self.params['gamma'+str(i+1)]
beta=self.params['beta'+str(i+1)]
bn=self.bn_params[i]
out,cache[i]=affine_batchnorm_relu_forward(out,W,b,gamma,beta,bn)
elif self.normalization=="layernorm":
gamma=self.params['gamma'+str(i+1)]
beta=self.params['beta'+str(i+1)]
bn=self.bn_params[i]
out,cache[i]=affine_layernorm_relu_forward(out,W,b,gamma,beta,bn)
else:
out, cache[i] = affine_relu_forward(out,W,b)
if self.use_dropout:
out, do_cache[i] = dropout_forward(out, self.dropout_param)
scores=out
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
############################################################################
# END OF YOUR CODE #
############################################################################
# If test mode return early.
if mode == "test":
return scores
loss, grads = 0.0, {}
############################################################################
# TODO: Implement the backward pass for the fully connected net. Store the #
# loss in the loss variable and gradients in the grads dictionary. Compute #
# data loss using softmax, and make sure that grads[k] holds the gradients #
# for self.params[k]. Don't forget to add L2 regularization! #
# #
# When using batch/layer normalization, you don't need to regularize the #
# scale and shift parameters. #
# #
# NOTE: To ensure that your implementation matches ours and you pass the #
# automated tests, make sure that your L2 regularization includes a factor #
# of 0.5 to simplify the expression for the gradient. #
############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
weight_sum_squared=0
for i in range(self.num_layers):
weight_sum_squared+=np.sum(np.square(self.params['W'+str(i+1)]))
loss,dx = softmax_loss(scores,y)
loss+=self.reg*0.5*weight_sum_squared
for i in reversed(range(self.num_layers)):
if i == self.num_layers-1: #last layer doesn't need relu, so just affine backward is enough.
dx, dW, db = affine_backward(dx,cache[i])
grads['W'+str(i+1)] = dW+self.reg*self.params['W'+str(i+1)]
grads['b'+str(i+1)] = db
else:
if self.use_dropout:
dx = dropout_backward(dx, do_cache[i])
if self.normalization == 'batchnorm':
dx, dW, db, dgamma, dbeta = affine_batchnorm_relu_backward(dx,cache[i])
grads['W'+str(i+1)] = dW+self.reg*self.params['W'+str(i+1)]
grads['b'+str(i+1)] = db
grads['gamma'+str(i+1)] = dgamma
grads['beta'+str(i+1)] = dbeta
elif self.normalization=="layernorm":
dx, dW, db, dgamma, dbeta=affine_layernorm_relu_backward(dx,cache[i])
grads['W'+str(i+1)]=dW+self.reg*self.params['W'+str(i+1)]
grads['b'+str(i+1)]=db
grads['gamma'+str(i+1)]=dgamma
grads['beta'+str(i+1)]=dbeta
else:
dx, dW, db = affine_relu_backward(dx,cache[i])
grads['W'+str(i+1)] = dW+self.reg*self.params['W'+str(i+1)]
grads['b'+str(i+1)] = db
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
############################################################################
# END OF YOUR CODE #
############################################################################
return loss, grads
FullyConnectedNet은 {affine- [batch/layer norm] - relu - [dropout]} x (L-1) - affine - softmax 로 구성됩니다. 구성에 맞게 파라미터 생성, forward, backward를 구현합니다.
def affine_batchnorm_relu_forward(x, w, b, gamma, beta, bn_params):
a, fc_cache = affine_forward(x,w,b)
an, bn_cache = batchnorm_forward(a, gamma, beta, bn_params)
out, relu_cache = relu_forward(an)
cache = (fc_cache, bn_cache, relu_cache)
return out, cache
def affine_batchnorm_relu_backward(dout, cache):
fc_cache, bn_cache, relu_cache = cache
da = relu_backward(dout, relu_cache)
dan, dgamma, dbeta = batchnorm_backward(da, bn_cache)
dx, dw, db = affine_backward(dan, fc_cache)
return dx, dw, db, dgamma, dbeta
def affine_layernorm_relu_forward(x, w, b, gamma, beta, bn_params):
a, fc_cache = affine_forward(x,w,b)
an, bn_cache = layernorm_forward(a, gamma, beta, bn_params)
out, relu_cache = relu_forward(an)
cache = (fc_cache, bn_cache, relu_cache)
return out, cache
def affine_layernorm_relu_backward(dout, cache):
fc_cache, bn_cache, relu_cache = cache
da = relu_backward(dout, relu_cache)
dan, dgamma, dbeta = layernorm_backward(da, bn_cache)
dx, dw, db = affine_backward(dan, fc_cache)
return dx, dw, db, dgamma, dbeta
affine forward, affine batchnorm relu forward, dropout 등의 함수를 사전에 정의하고 사용해줍니다. (batchnorm, dropout 은 다음 과제를 진행하며 구현하고 사용해줍니다.)
sgd_moment 는 아래와 같습니다.
def sgd_momentum(w, dw, config=None):
"""
Performs stochastic gradient descent with momentum.
config format:
- learning_rate: Scalar learning rate.
- momentum: Scalar between 0 and 1 giving the momentum value.
Setting momentum = 0 reduces to sgd.
- velocity: A numpy array of the same shape as w and dw used to store a
moving average of the gradients.
"""
if config is None:
config = {}
config.setdefault("learning_rate", 1e-2)
config.setdefault("momentum", 0.9)
v = config.get("velocity", np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the momentum update formula. Store the updated value in #
# the next_w variable. You should also use and update the velocity v. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
v = config['momentum']*v - config['learning_rate']*dw
next_w = w+v
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
config["velocity"] = v
return next_w, config
SGD는 일반적으로 알고있는 경사하강법 방법입니다.
x += learning_rate * $\frac{\partial L}{\partial x}$
SGD + Momentum은 learning_rate * Velocity(dw의 누적합)를 learning step으로 사용합니다.
수식은 아래 CS231n 강의 자료를 살펴보면 이해하기 편합니다.

RMSProp과 Adam은 아래와 같습니다.
def rmsprop(w, dw, config=None):
"""
Uses the RMSProp update rule, which uses a moving average of squared
gradient values to set adaptive per-parameter learning rates.
config format:
- learning_rate: Scalar learning rate.
- decay_rate: Scalar between 0 and 1 giving the decay rate for the squared
gradient cache.
- epsilon: Small scalar used for smoothing to avoid dividing by zero.
- cache: Moving average of second moments of gradients.
"""
if config is None:
config = {}
config.setdefault("learning_rate", 1e-2)
config.setdefault("decay_rate", 0.99)
config.setdefault("epsilon", 1e-8)
config.setdefault("cache", np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the RMSprop update formula, storing the next value of w #
# in the next_w variable. Don't forget to update cache value stored in #
# config['cache']. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
config['cache'] = config['decay_rate']*config['cache'] + (1-config['decay_rate'])*dw**2
next_w = w - config['learning_rate']*dw / (np.sqrt(config['cache'])+config["epsilon"])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, config
def adam(w, dw, config=None):
"""
Uses the Adam update rule, which incorporates moving averages of both the
gradient and its square and a bias correction term.
config format:
- learning_rate: Scalar learning rate.
- beta1: Decay rate for moving average of first moment of gradient.
- beta2: Decay rate for moving average of second moment of gradient.
- epsilon: Small scalar used for smoothing to avoid dividing by zero.
- m: Moving average of gradient.
- v: Moving average of squared gradient.
- t: Iteration number.
"""
if config is None:
config = {}
config.setdefault("learning_rate", 1e-3)
config.setdefault("beta1", 0.9)
config.setdefault("beta2", 0.999)
config.setdefault("epsilon", 1e-8)
config.setdefault("m", np.zeros_like(w))
config.setdefault("v", np.zeros_like(w))
config.setdefault("t", 0)
next_w = None
###########################################################################
# TODO: Implement the Adam update formula, storing the next value of w in #
# the next_w variable. Don't forget to update the m, v, and t variables #
# stored in config. #
# #
# NOTE: In order to match the reference output, please modify t _before_ #
# using it in any calculations. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
config["t"]+=1
config["m"] = config["beta1"]*config["m"] + (1-config["beta1"])*dw
mt = config["m"] / (1-config["beta1"]**config["t"])
config["v"] = config["beta2"]*config["v"] + (1-config["beta2"])*(dw**2)
vt = config["v"] / (1-config["beta2"]**config["t"])
next_w = w- ((config["learning_rate"] * mt) / (np.sqrt(vt) + config["epsilon"]))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, config
위 내용은 CS231n 강의 중 RSMProp과 Adam 슬라이드를 참고하면 이해하기 편합니다.

RMSProp은 gradient가 큰 방향에서는 learning_step을 줄이고, gradient가 작은 방향에서는 learning_step을 높여 학습하는 방법입니다.
gradient의 제곱을 누적 합으로 계산한 뒤, 루트를 씌워 나눠줍니다.
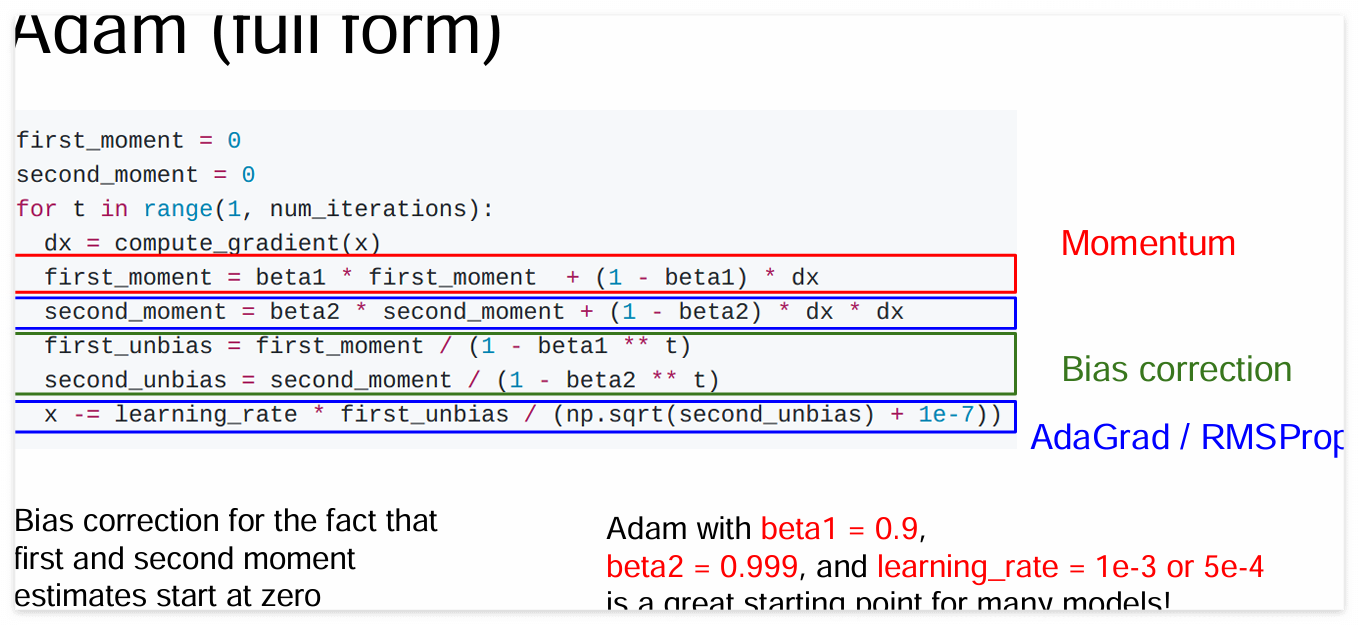
Adam은 Momentum과 RMSProp, Bias correction 방법이 모두 합쳐진 방법입니다.
Momentum과 RMSProp은 위의 내용과 같습니다. Bias correction은 초기 first_unbias, second_unbias이 매우 작은 점을 보정하기 위해 (1 - beta ** t) 로 나눠줍니다. t는 가중치 업데이트 횟수 입니다.
best_model = None
################################################################################
# TODO: Train the best FullyConnectedNet that you can on CIFAR-10. You might #
# find batch/layer normalization and dropout useful. Store your best model in #
# the best_model variable. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
from itertools import product
np.random.seed(42)
#Params
lr = [0.0005, 0.0008]
reg = [0.01]
decay = [0.95]
drop = [0.78]
arch = [[64, 64, 64]]
params = product(arch, reg, drop, lr)
# Architecture
h_number = [2, 3, 4, 5]
h_size = [32, 64, 128]
val_acc = 0
for param in list(params):
print('arch:', param[0])
print('regularization:', param[1])
print('dropout', param[2])
print('learning_rate:', param[3])
model = FullyConnectedNet(param[0], weight_scale=2e-2,
reg=param[1], dropout_keep_ratio=param[2],
normalization='batchnorm')
solver = Solver(model, data,
num_epochs=20, batch_size=100,
update_rule='adam', lr_decay=0.95,
optim_config={
'learning_rate': param[3],
},
verbose=False)
solver.train()
print('acc', solver.best_val_acc)
if solver.best_val_acc > val_acc:
val_acc = solver.best_val_acc
best_model = model
lr = solver.optim_config['learning_rate']
print('-------------------')
print('Best acc:', val_acc)
print('learning_rate:', lr)
print('regularization:', best_model.reg)
print('dropout', best_model.dropout_param['p'])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################

최종적으로 하이퍼 파라미터 튜닝을 통해 Validation set accuracy를 50% 이상으로 올려줍니다.
'Stanford CS231n' 카테고리의 다른 글
| CS231n Assignment 2(3) : Dropout (0) | 2024.12.18 |
|---|---|
| CS231n Assignment 2(2) : BatchNormalization (0) | 2024.12.18 |
| CS231n Assignment 1(3) : Implement a Softmax classifier (0) | 2024.12.08 |
| CS231n Assignment 1(1) : K-Nearest Neighbor classifier (0) | 2024.12.04 |
| Lecture 11: Detection and Segmentation (1) | 2024.11.26 |