Stanford에서 강의하는 CS231n의 Assignment 1(1): KNN을 정리한 글입니다.
Inline Question 1
Notice the structured patterns in the distance matrix, where some rows or columns are visibly brighter. (Note that with the default color scheme black indicates low distances while white indicates high distances.)
1) What in the data is the cause behind the distinctly bright rows?
2) What causes the columns?
Your Answer : 1. distance matrix의 각 행(row)은 단일 테스트 샘플과 모든 훈련 샘플 간의 거리를 나타냅니다. 테스트 샘플이 훈련 샘플과 픽셀 값에서 차이가 클수록 $L_2$ 가 더 커지며, 더 밝게 보입니다.
2. 마찬가지로, 단일 훈련 샘플과 테스트 샘플 간의 $L_2$ 는 열(column)로 표현되며, 더 큰 distance는 더 밝게 보입니다.
Inline Question 2
We can also use other distance metrics such as L1 distance. For pixel values $p^{(k)}_{ij}$ at location $(i,j)$ of some image $I_k$, the mean $\mu$ across all pixels over all images is
$$\mu = \frac{1}{nhw}\sum^n_{k=1}\sum^h_{i=1}\sum^w_{j=1}p^{(k)}_{ij}$$
And the pixel-wise mean $\mu_{ij} $ across all images is
$$\mu_{ij} = \frac{1}{n}\sum^n_{k=1}p^{(k)}_{ij}$$ The general standard deviation σ and pixel-wise standard deviation σij is defined similarly.
Which of the following preprocessing steps will not change the performance of a Nearest Neighbor classifier that uses L1 distance? Select all that apply. To clarify, both training and test examples are preprocessed in the same way.
1. Subtracting the mean $\mu$
2. Subtracting the per pixel mean $\mu_{ij}$
3. Subtracting the mean μ and dividing by the standard deviation σ.
4. Subtracting the pixel-wise mean μij and dividing by the pixel-wise standard deviation $\mu_{ij}$.
5. Rotating the coordinate axes of the data, which means rotating all the images by the same angle. Empty regions in the image caused by rotation are padded with a same pixel value and no interpolation is performed.
Your Answer : 1, 2, 3, 5(?)
Your Explanation :
1., 2. $x^i$와 $x^j$에 동일하게 평균을 빼줬으므로 distance는 보존됩니다. pixel별 평균을 빼줬을때도 동일합니다.
$$||(x^{(i)} - \bar{x}) - (x^{(j)} - \bar{x})||_1 = ||x^{(i)} - x^{(j)}||_1 $$
3. 동일한 $\mu$로 나누어줬기 때문에 distance는 scaling의 효과만 있고, 상대적 차이는 보존됩니다.
$$||\frac{x^{(i)} - \bar{x}}{\mu} - \frac{x^{(j)} - \bar{x}}{\mu}||_1 \leq ||\frac{x^{(i)} - \bar{x}}{\mu} - \frac{x^{(k)} - \bar{x}}{\mu}||_1 $$
$$\frac{1}{\mu}||x^{(i)} - x^{(j)}||_1 \leq \frac{1}{\mu}||x^{(i)} - x^{(k)}||_1 $$
4. $\frac{1}{\mu_{ij}}$ 와 $\frac{1}{\mu_{ik}}$ 의 크기에 따라 두 distance의 상대적 차이가 변할 수 있습니다.
$$\frac{1}{\mu_{ij}}||x^{(i)} - x^{(j)}||_1 \leq \frac{1}{\mu_{ik}}||x^{(i)}-x^{(k)}||$$
5. Train 이미지와 Test 이미지를 동일한 각도로 회전하였을 때 동일한 픽셀을 빼주기 때문에 L1 Loss는 변하지 않습니다.
2차원 이상의 좌표계에서의 점들에 대해서 좌표계가 회전했을 때에는 좌표들 간의 L1 Loss가 변합니다. 좌표계에서의 L1 loss는 '좌표' 에 관련이 있습니다. 하지만, 이미지에서의 L1 Loss는 '픽셀' 에 관련이 있습니다. '픽셀'은 축이 회전한다고 해서 변하지 않습니다. 더불어, 훈련 데이터셋과 테스트 데이터셋 전부 같은 각도로 회전한다고 하면 L1 Loss는 변하지 않을 것 입니다.
Inline Question 3
Which of the following statements about k-Nearest Neighbor (k-NN) are true in a classification setting, and for all k? Select all that apply.
1. The decision boundary of the k-NN classifier is linear.
2. The training error of a 1-NN will always be lower than or equal to that of 5-NN.
3. The test error of a 1-NN will always be lower than that of a 5-NN.
4. The time needed to classify a test example with the k-NN classifier grows with the size of the training set.
5. None of the above.
Your Answer : 2, 4
Your Explanation :
1. linear classifier는 보통 feature space에서의 결정 경계를 초평면(hyperplane)으로 분리할 수 있다는 뜻입니다. KNN의 경우 초평면이 존재하지 않습니다.
2. 1-NN은 training error가 0입니다. 하지만, 5-NN의 경우 training error가 0이 아닐 수 있습니다.
3. 위의 예제를 통해 1-NN보다 5-NN의 테스트 성능이 좋은 걸 확인했습니다.
4. 예측 단계에서 테스트 데이터들은 모든 학습 데이터들과 distance를 계산해야하기 때문에 시간이 증가합니다.
Code
첫 번째 Implementation 조건은 다음과 같다.
- test 데이터와 train 데이터들의 distance matrix 구하는 함수 구현
- 학습 데이터 : Self.X_train (5000x3072), 테스트 데이터 : X (500x3072)
- 2 번의 반복문을 통해 구할 것
학습 데이터와 테스트 데이터들 간의 distance matrix를 구해야 한다. 학습 데이터는 총 5000개, 테스트 데이터는 500개 이므로 500x5000 matrix(또는 5000x500 matrix) 가 output임을 생각할 수 있다. 문제에서 dists = np.zeros((num_test, num_train)) 으로 500x5000을 주었으며, 이 matrix를 채우면 된다.
이중 포문으로 구성되어 있으니, 2차원 배열의 각 원소에 직접 접근하여 값을 채워 넣는다.
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension, nor use np.linalg.norm(). #
#####################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i, j] = np.sqrt(np.sum(np.square(self.X_train[j]-X[i])))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
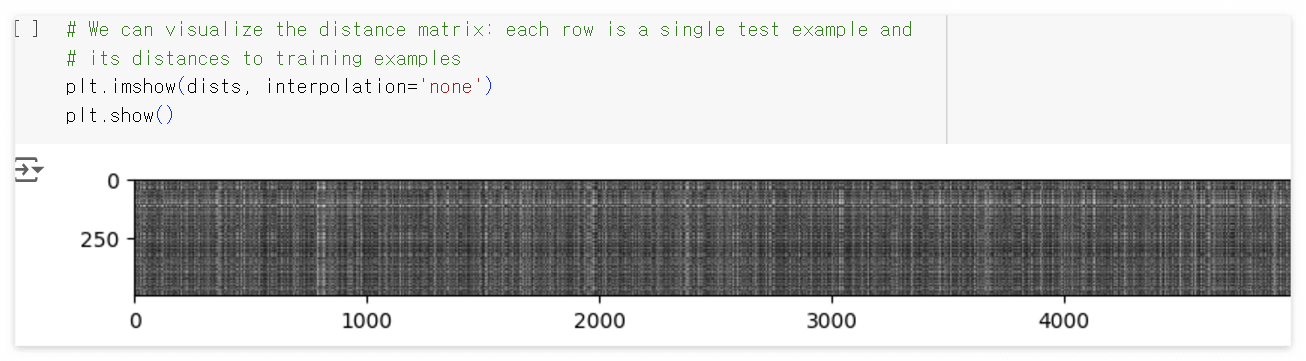
이렇게 구한 distance matrix를 시각화 해보면 다음과 같이 나온다.
matrix의 행은 각 테스트 데이터와 모든 학습 데이터들과의 L2 distance 로 이루어져 있다. 가령, 0번째 행의 5000개 데이터는 0번째 테스트 데이터와 5000개의 학습 데이터들과의 L2 distance이다.
distance matrix를 계산했으니, test data에 label을 부여할 수 있는 predict_labels 함수를 채워보자.
- 각 행에서 L2 distance를 Sorting 한 뒤, index를 저장한다.
- (1) 에서 저장한 index를 통해 L2 distance가 가장 낮은 index를 K개 찾는다.
- 이 때, index는 학습 데이터의 위치이다.
- K개의 다수결(최빈값)을 y_pred[i] 로 결정한다.
- y_pred[i] 는 $i$ 번째 테스트 데이터이다.
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists_indices = np.argsort(dists[i])
dists_label_list = [self.y_train[n] for n in dists_indices[:k]]
y_pred[i] = np.argmax(np.bincount(dists_label_list))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return y_pred

Compute_distances_two_loops 함수와 predict_labels 함수를 구현 하고 난 뒤, K=1 과 K=5 일 때의 성능을 구해본다. 과제의 description에 나와있는 성능과 일치했으므로 잘 구현했으리라 믿는다.
이후, Compute_distances_two_loops 함수를 좀 더 간단하게 한번의 반복문을 통한 구현과, 반복문이 없이 함수를 구현해보자.
한번의 반복문을 통해 구현하는 것은 이중 포문을 통해 구현하는 것과 크게 다른 점은 없다.
- Test 데이터의 개수 만큼(500)번 반복
- Train 데이터(5000, 3072)와 Test 데이터(1, 3072)의 sub 연산을 통해 distance matrix (1, 5000) 생성
- (주의할 점) np.sum() 함수를 사용할 때 axis=1을 지정해줘야 한다. axis=1을 지정하지 않으면 모든 행의 합(=Scalar) 값이 나오게 됨
반복이 끝나면 (500, 5000) 크기의 distance matrix가 생성된다.
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i] = np.sqrt(np.sum(np.square(self.X_train - X[i]), axis=1))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
반복문 없이 함수를 구현하기 위해선 새로운 접근법이 필요하다. Hint 에 broadcast연산이 적혀 있어서 뭔가 알 수 없는 파이썬 만의 계산 방법이 있는 줄 알았다. (하지만 그게 아니라, 단순히 수식을 풀어 쓰면 되는거였다..ㅜ broadcast 연산은 생각해보니 One_loop 함수에서도 적용되고 있었다..)
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists = np.sqrt(np.reshape(np.sum(np.square(X), axis=1), (num_test, -1)) + np.reshape(np.sum(np.square(self.X_train), axis=1), (-1, num_train)) - 2*(np.dot(X, np.transpose(self.X_train))))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
코드가 가독성이 떨어져 보일 수 있지만, 이해하고 나면 어렵지 않다.
L2 distance 수식을 전개하면 아래와 같다.
$dist_{L2} = \sqrt{\sum^n_i(x_i-y_i)^2} = \sqrt{\sum^n_i x^2_i + \sum^n_i y^2_i - \sum^n_i 2x_iy_i}$
이를 통해 이중 포문 없이 한번에 계산이 가능하다.
다음은 Cross-validation 이다.
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
accuracy_temp = []
for fold in range(num_folds):
X_test_fold = X_train_folds[fold]
y_test_fold = y_train_folds[fold]
X_train_fold = np.vstack([X_train_folds[j] for j in range(num_folds) if j != fold])
y_train_fold = np.vstack([y_train_folds[j] for j in range(num_folds) if j != fold]).reshape(-1,)
classifier.train(X_train_fold, y_train_fold)
y_test_pred = classifier.predict(X_test_fold, k=k)
num_correct = np.sum(y_test_pred == y_test_fold)
accuracy_temp.append(num_correct/len(y_test_pred))
k_to_accuracies[k] = accuracy_temp
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))
Cross validation의 개념을 이해하고 있다면 어렵지 않다. num_fold 개수 만큼 Train data를 split 한 뒤, 하나의 서브 샘플을 제외한 나머지를 학습에, 하나의 서브 샘플을 예측에 사용한다.
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
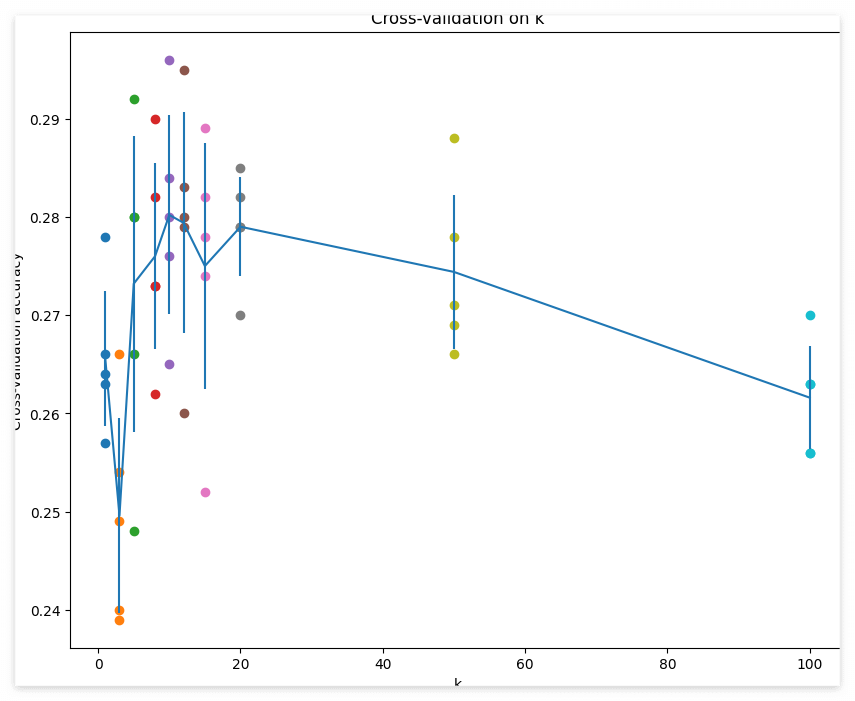
시각화를 통해 K에 따른 accuracy를 확인한다.
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = k_choices[accuracies_mean.argmax()]
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
Got 141 / 500 correct => accuracy: 0.282000
accuracies_mean의 argmax를 통해 가장 성능이 좋았던 k의 index를 가져온 뒤 best_k로 지정한다.
Inline Question 및 Code는 실제 정답과 차이가 있을 수 있습니다.
궁금한 점이나 틀린 점이 있다면 댓글로 알려주시면 감사드리겠습니다. :)
'Stanford CS231n' 카테고리의 다른 글
| CS231n Assignment 2(1) : Multi-Layer Fully Connected Neural Networks (1) | 2024.12.17 |
|---|---|
| CS231n Assignment 1(3) : Implement a Softmax classifier (0) | 2024.12.08 |
| Lecture 11: Detection and Segmentation (1) | 2024.11.26 |
| Weight Initialization (0) | 2024.11.11 |
| Lecture 10: Recurrent Neural Networks (2) | 2024.11.11 |