Stanford에서 강의하는 CS231n에 대해서 공부하고 정리한 글입니다.
Slide: PowerPoint Presentation
이번 정리는 CS231n 2017년도 강의 Lecture 6: Training Neural Networks 1 의 Weight Initialization 부분을 조금 더 정리해보고자 작성하였습니다.
강의 자료는 2024년도 CS231n 강의 Lecture 6 (Part 2): Training Neural Networks를 사용하였습니다.

우리가 처음 어떤 네트워크에 대해 설계했다고 해보자.
그렇다면, 이 모델을 학습시키기 위한 초기값들을 세팅해주어야 한다.
우리는 모델의 파라미터 $w$의 초기값을 설정해줘야 한다.

첫 번째 Idea는 $w$를 랜덤한 작은 값들로 세팅해보는 것이다.
하지만, 이는 Small network에서는 잘 작동할 수 있을지는 몰라도, Deeper network에서는 문제가 발생할 수 있다.
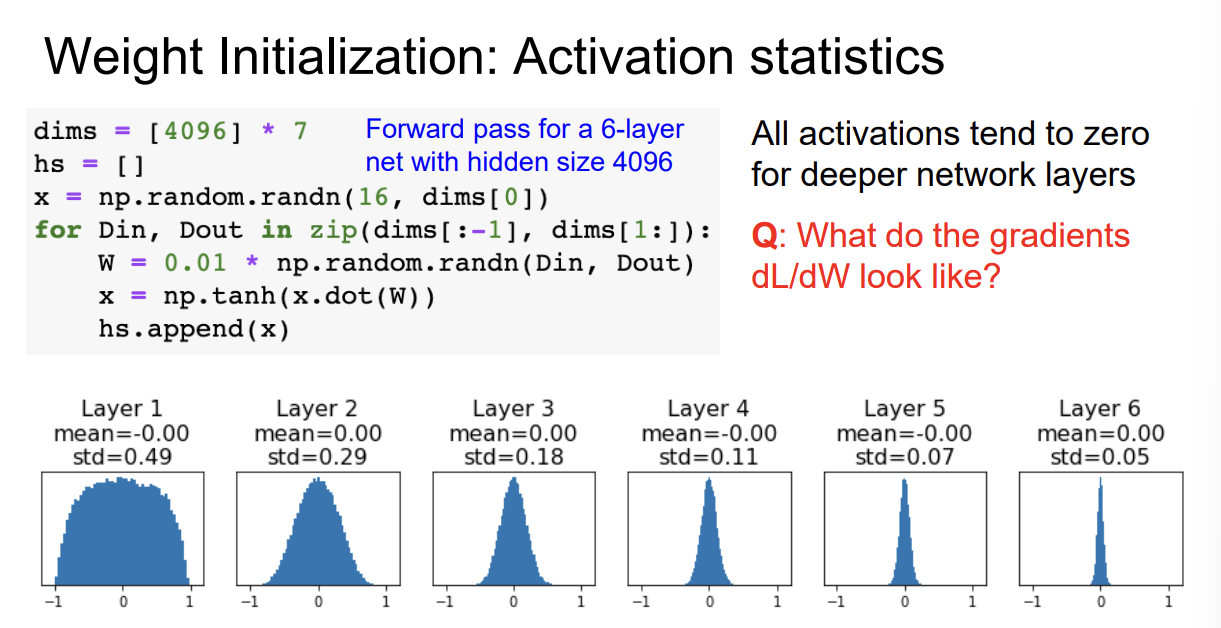
예를 들어보자.
이 예제에선 $tanh$ 함수를 Activation function으로 사용했다.
예제의 layer별 activation function의 출력 분포를 표현된 그림을 살펴보자.
activation function의 출력 분포는 점점 0에 치우친다.
이것은 $tanh$ 함수가 Zero-centered 특징을 갖고 있으면서, 레이어를 지나며 매우 작은 가중치들이 곱해지기 때문이다.
그렇다면, Backpropagation에서 $\frac{\partial L}{\partial W}$ 는 어떻게 될까?

아마, 거의 모든 gradient가 0이 될 것이다.
$f = wx$ Gate를 생각해보자.
$\frac{\partial f}{\partial w} = x$임을 알 수 있다.
이는 $w$의 gradient가 $x$ 와 연관있음을 알 수 있다.
이 때, $x$는 매우 작은 값이기 때문에 gradient가 0에 가까울 것이다.

가중치가 임의의 큰 값인 경우는 어떨까?
거의 모든 뉴런의 출력이 -1 또는 1이 된다.
입력 값들이 큰 값의 가중치들과 곱해져 값이 발산하게 되는데, $tanh$의 범위가 [-1, 1] 이기 때문이다.
이런 경우 local gradient가 대부분 0 또는, 0에 가까운 값이 되며 학습이 일어나지 않는다.
우리는, 입력과 출력의 분포가 바뀔 때 문제가 발생하는 것을 알 수 있다.
(이는, 특히 Deep Neural Network 에서 문제가 심해진다.)
따라서, 입력과 출력의 분포가 같거나, 적절히 가우시안 분포를 따르게 강제해주는 초기화 방식을 사용하고자 한다.

그 중 하나가 "Xavier" Initialization 이다.
Xavier initialization의 가정은 다음과 같다.
- 입력 데이터와 가중치가 Zero-Centered 되어 있다.
- 입력 데이터와 가중치는 서로 독립적이며 동일한 분포를 따른다.
- Bias는 0으로 초기화 된다.
다음 입력을 사용하여 $Var(W)$를 유도해보자.
$$z = w_1a_1 + w_2a_2 + ... + w_na_n$$

$$Var(z) = \sum^{n}_{j=1} w_{ij}a_{j}$$
$$Var(z) = \sum^{n}_{j=1} E[w_{ij}]^2 Var(a_j) + E[a_j]^2 Var(w_{ij}) + Var(w_{ij}) Var(a_j)$$
이며, 평균이 0이기 때문에
$$Var(z) = nVar(w_{ij})Var(a_j)$$
이고, $Var(z) = Var(a) $ 라고 가정하였으므로, 양 변을 소거하면
$$Var(w) = \frac{1}{n}$$
을 얻을 수 있다.
즉, 입력과 출력의 분산이 같기 위해선 가중치 $w$의 분산이 $n$ 에 반비례하면 된다.
W = np.random.rand(Din, Dout) / np.sqrt(Din)
따라서, 우리는 다음과 같은 $W$ 초기화를 통해 입력과 출력의 분산을 맞춰줄 수 있게 된다.

그런데, 이런 가중치 초기화 방법은 ReLU에선 먹히지 않는다.
Activation Function이 ReLu일때는 입력의 Negative 영역의 값들이 모두 0이 된다.
이런 한계점을 개선한 방식이 He Initialization 이다.

Xavier Initialization이 가중치의 분산을 $\frac{1}{n}$로 두었다면,
He Initialization은 가중치의 분산을 $\frac{2}{n}$로 한다.
ReLU의 특성상 출력이 0에 몰려 있지만, 나머지 데이터는 Positive 영역에서 골고루 퍼져 있음을 확인할 수 있다.
'Stanford CS231n' 카테고리의 다른 글
| CS231n Assignment 1(1) : K-Nearest Neighbor classifier (0) | 2024.12.04 |
|---|---|
| Lecture 11: Detection and Segmentation (1) | 2024.11.26 |
| Lecture 10: Recurrent Neural Networks (2) | 2024.11.11 |
| Lecture 9: CNN Architectures (1) | 2024.11.11 |
| Lecture 7: Training Neural Networks 2 (1) | 2024.11.08 |